1, 题目背景
他想停下,但是马群奇怪地沉默着。
他不敢打破这奇怪的寂静。
他跑得麻木了。他甚至觉得,自己可以把眼睛闭上。
就在这时,他仿佛真的从前方看到了光,那永恒的,无限追求的光。
他便也沉寂了下来,心安理得地,像其他马那样。
又一次的日出,便笼罩在了这寂静的草原上。
2,题目描述
这匹马(我们姑且称其为Kirito)想起了若干年以前的一次探险。
那是一个偏远而又神秘的国家。
因为国家是在深山里的,开凿联通城市的道路非常不容易,所以,他们建了最少条数的道路,把所有城市都连了起来。也就是说,这个国家城市之间道路的联系形成了一棵树,每条路的长度都是$1$。
在前往那个国家之前,Kirito购买了一份这个国家的地图。他发现,每个城市都有一个因为他本身的历史文化而具有的基础魅力值$a_i$,但是一个城市真正的魅力还取决于它的繁华程度。具体地,一个节点$u$会给他到首都的最短路径上的所有城市再贡献$a_u$点魅力值(不会再给自己贡献,但是会给首都贡献)。
因此,一个城市的魅力值$f_i$就是它的基础魅力值再加上其他城市给他贡献的魅力值之和。
现在,Kirito想规划一条旅行线路。因为他不是什么毒瘤,所以这条线路一定是从起点到终点的简单路径。
因为不想让自己一开始就受不了或者心理落差太大,作为起点的城市的不能是这条路径经过的所有城市的的最大值或者最小值。
比如,一条由$2$至$4$的路径,经过城市2 − > 3 − > 1 − > 4,其中$f_2=2,f_3=3,f_1=4,f_4=2$,这条路径就不行。
现在,每座城市有一个估价函数$g_i$,表示从第i座城市出发,能按照上面的规则到达的所有城市的f值依次按位或(即$or$或者|)得到的值。
Kirito认为这个函数能很好地反应这个城市到底好不好(不接受反驳)。如果一个城市 都不能到达,g就是0。比如,1号城市能到达2,3,4号城市。其中$f_2=2,f_3=3,f_4=5$,那么$g_1=2|3|5=7$。 现在,Kirito会把城市之间的关系、首都是几号城市,以及每座城市的$a_i$给你,请你帮 他计算每座城市的$g$是多少。(救救孩子)
3,输入输出
输入格式
第一行两个正整数$n, capi$,表示城市数和首都编号。
接下来$n-1$行,每行两个数u, v,表示有一条连接u, v的树边。
接下来一行n个正整数$a_i$,表示每个城市的基础魅力值
输出格式
一行n个整数,第i个表示$g_i$。
输入样例
7 1
1 2
2 3
1 4
4 6
4 7
7 5
2 1 2 1 1 2 1
输出样例
0 3 1 3 0 1 0
4,题解
40%做法
我们根据题意处理出$f_i$(这个爱怎么处理怎么处理,树形DP或者树剖暴力修改都可以)。然后……爆搜即可。
100%做法
好像跳了很多步骤分?说实话那些分在没想到正解的时候不太好拿,分值还低。
我们先画出样例的图像
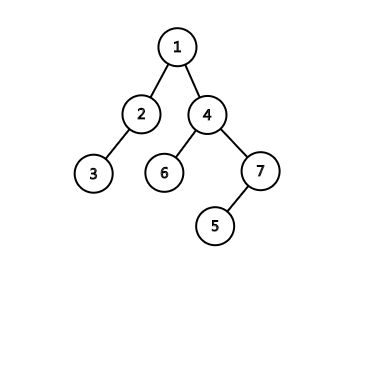
由题意知,所有节点的额外贡献由于向着根节点,导致$f_{fa}>=f_{son}$。
可以推出一个简单规律:
定义向上为向父亲节点方向走,那么向上的节点$f$值一定大于向下的节点。
通过这个规律转化题意——既然起点不能是最大或最小,那么我们先要走到一个更大的节点,再走到一个更小的节点。即,向上走,再向下走。
以2出发,一个可能的图长这样。
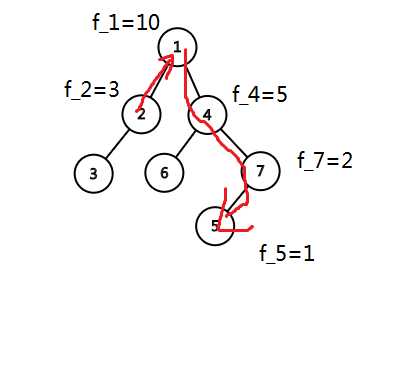
我们先向上走,再向下走,直到走到$f_{ed} 从另一个角度想,我们就是要找那些不在$st$子树内部,而值又小于$st$的点。 问题便迎刃而解。判断子树内部可以用dfs序,问题变成了维护偏序问题。 之后想用怎样的数据结构搞就随便了。都是先使一维有序,再用数据结构维护另一维。 我这里是对$val$排序,用线段树维护在$val_{st}$左边(即值更小)且不在子树内部的点的“或和”。 代码有点臃肿难看,敬请见谅。#include <bits/stdc++.h>
using namespace std;
inline int red(){
int x=0,f=1;char ch=getchar();for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-1;
for(;isdigit(ch);ch=getchar())x=x*10+ch-'0';return x*f;
}
const int N = 5e5+10;
struct edge{int u,v,nxt;}e[N<<1];
int head[N],du[N],add_cnt;
inline void add(int u,int v){e[++add_cnt]=(edge){u,v,head[u]};head[u]=add_cnt;++du[u];}
int n,root;
int ori[N],ans[N];
int fa[N],dep[N],sze[N],son[N],dfn[N];
int top[N],idx[N],rnk[N],tot,cnt;
namespace SGT{
int val[N<<2],lzy[N<<2];
#define ls (o<<1)
#define rs (o<<1|1)
#define mid (tl+tr>>1)
void pushup(int o){val[o]=val[ls]+val[rs];}
void pushup2(int o){val[o]=val[ls]|val[rs];}
void pushdown(int o,int tl,int tr){
if(!lzy[o]) return;
lzy[ls]+=lzy[o],lzy[rs]+=lzy[o];
val[ls]+=lzy[o]*(mid-tl+1),val[rs]+=lzy[o]*(tr-mid);
lzy[o]=0;
}
void update2(int o,int tar,int tl,int tr,int va){
if(tl==tr){val[o]|=va;return;}
if(tar<=mid) update2(ls,tar,tl,mid,va);
else update2(rs,tar,mid+1,tr,va);
pushup2(o);
}
void update(int o,int l,int r,int tl,int tr,int va){
if(l<=tl&&tr<=r){lzy[o]+=va,val[o]+=va*(tr-tl+1);return;}
pushdown(o,tl,tr);
if(l<=mid) update(ls,l,r,tl,mid,va);
if(r>mid) update(rs,l,r,mid+1,tr,va);
pushup(o);
}
int query2(int o,int l,int r,int tl,int tr){
if(l<=tl&&tr<=r) return val[o];
int ret=0;pushup2(o);
if(l<=mid) ret|=query2(ls,l,r,tl,mid);
if(r>mid) ret|=query2(rs,l,r,mid+1,tr);
return ret;
}
int query(int o,int l,int r,int tl,int tr){
if(l<=tl&&tr<=r) return val[o];
pushdown(o,tl,tr),pushup(o);
int ret=0;
if(l<=mid) ret+=query(ls,l,r,tl,mid);
if(r>mid) ret+=query(rs,l,r,mid+1,tr);
return ret;
}
}
void dfs1(int u,int f,int d){
fa[u]=f,dep[u]=d,sze[u]=1;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;if(v==f) continue;
dfs1(v,u,d+1);
sze[u]+=sze[v];
if(sze[v]>sze[son[u]]) son[u]=v;
}
}
void dfs2(int u,int tp){
top[u]=tp,idx[u]=++tot,rnk[tot]=u;
if(son[u]) dfs2(son[u],tp);
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(v!=fa[u]&&v!=son[u]) dfs2(v,v);
}
}
void dfsn(int u){
dfn[u]=++cnt;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;if(v==fa[u]) continue;
dfsn(v);
}
}
void update(int x,int y,int va){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
SGT::update(1,idx[top[x]],idx[x],1,n,va);
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
SGT::update(1,idx[x],idx[y],1,n,va);
}
void build(int o,int tl,int tr){
if(tl==tr){SGT::val[o]=ori[rnk[tl]];return;}
build(ls,tl,mid),build(rs,mid+1,tr);
SGT::pushup(o);
}
void build2(int o,int tl,int tr){
SGT::lzy[o]=SGT::val[o]=0;
if(tl==tr){SGT::lzy[o]=SGT::val[o]=0;return;}
build2(ls,tl,mid),build2(rs,mid+1,tr);
SGT::pushup2(o);
}
struct node{int val,id;}t[N];
bool cmp(node a,node b){return a.val<b.val;}
queue<int>q;
int main(){
int size=128<<20;
__asm__ ("movq %0,%%rsp\n"::"r"((char*)malloc(size)+size));
n=red(),root=red();
for(int i=1;i<n;++i){
int u=red(),v=red();
add(u,v),add(v,u);
}
for(int i=1;i<=n;++i) ori[i]=red();
dfs1(root,0,1),dfs2(root,root),dfsn(root);
build(1,1,n);
for(int i=1;i<=n;++i) if(i!=root) update(fa[i],root,ori[i]);
for(int i=1;i<=n;++i) t[i].val=SGT::query(1,idx[i],idx[i],1,n),t[i].id=i;
sort(t+1,t+n+1,cmp);
build2(1,1,n);
for(int i=1;i<=n;++i){
int u=t[i].id;
while(t[i].val!=t[i-1].val&&!q.empty()) SGT::update2(1,dfn[t[q.front()].id],1,n,t[q.front()].val),q.pop();
ans[u]|=SGT::query2(1,1,dfn[u],1,n);
ans[u]|=SGT::query2(1,dfn[u]+sze[u],n,1,n);
if(t[i].val!=t[i+1].val) SGT::update2(1,dfn[u],1,n,t[i].val);
else q.push(i);
}
for(int i=1;i<=n;++i) printf("%d ",ans[i]);
exit(0);
}

